三角形的面積可以通過(guò)以下公式來(lái)計(jì)算：
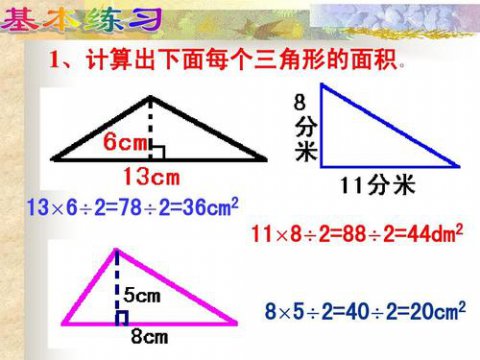
A = 1/2 * b * h
其中，A表示三角形的面積，b表示三角形底邊的長(zhǎng)度，h表示三角形頂點(diǎn)到底邊的垂線高度。
這個(gè)公式的推導(dǎo)可以通過(guò)將三角形劃分為兩個(gè)等腰三角形來(lái)實(shí)現(xiàn)。具體而言，我們可以假設(shè)b為底邊的長(zhǎng)度，h為頂點(diǎn)到底邊的垂線高度。然后，我們可以將三角形從垂線分為兩份，這樣就得到了兩個(gè)等腰三角形，它們的底邊長(zhǎng)度為b/2，高度為h。每個(gè)等腰三角形的面積為：
A = 1/2 * (b/2) * h = 1/4 * b * h
由此可見(jiàn)，兩個(gè)等腰三角形的面積之和為1/2 * b * h，即整個(gè)三角形的面積。
需要注意的是，如果我們無(wú)法直接測(cè)量三角形的高度，我們可以采用勾股定理來(lái)計(jì)算。勾股定理表明，在直角三角形中，斜邊的平方等于底邊長(zhǎng)度的平方加上高度的平方。如果我們知道三角形的兩條直角邊的長(zhǎng)度，可以用勾股定理來(lái)計(jì)算出斜邊的長(zhǎng)度，然后就可以根據(jù)底邊和高度來(lái)計(jì)算三角形的面積了。
除此之外，還有其他方法來(lái)計(jì)算三角形的面積，如海龍公式、正弦定理等。但是，這些方法都需要更多的知識(shí)和數(shù)學(xué)技巧，因此相對(duì)來(lái)說(shuō)較為復(fù)雜。如果想要更深入地了解這些方法，可以參考相關(guān)的課本或?qū)W習(xí)資料。
三角形的面積是通過(guò)以下公式計(jì)算的：面積 = 1/2 × 底邊長(zhǎng) × 高，其中“底邊長(zhǎng)”指的是三角形的一條邊，而“高”是從底邊垂直向上的線段所對(duì)應(yīng)的長(zhǎng)度。
可以通過(guò)以下步驟來(lái)計(jì)算三角形的面積：
1. 確定底邊長(zhǎng)：在三角形中，選擇一條邊作為底邊長(zhǎng)。
2. 確定高：從底邊長(zhǎng)的中點(diǎn)開(kāi)始垂直向上畫(huà)一條線段，該線段的長(zhǎng)度就是高。
3. 計(jì)算面積：將底邊長(zhǎng)和高代入公式中，計(jì)算出三角形的面積。
例如，假設(shè)有一個(gè)底邊長(zhǎng)為8厘米，高為4厘米的三角形，那么它的面積就是：
面積 = 1/2 × 8厘米 × 4厘米
= 16平方厘米
需要注意的是，在實(shí)際問(wèn)題中，需要根據(jù)具體情況選擇合適的計(jì)算方法來(lái)求解三角形的面積。例如，如果只知道三角形的三邊長(zhǎng)，可以通過(guò)海倫公式來(lái)求解面積；如果只知道三角形的兩條邊和它們之間的夾角，可以通過(guò)正弦定理或余弦定理來(lái)求解面積等。
